Sommaire
Application des 1ère et 2ème lois de Newton
L’exercice du skieur
Les différents types de mouvement
Exercice de l’igloo
Masses-poulie avec frottements
On se place dans le référentiel terrestre.
On considère une balle lâchée dans le vide sans vitesse initiale.
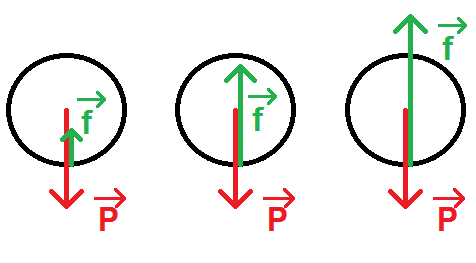
La balle est soumise à son poids et à des forces de frottements représentées sur les schémas.
1) Décrire le mouvement dans chacun des cas.
2) Dans quel(s) cas le principe d’inertie s’applique-t-il ?
On se place dans le référentiel terrestre.
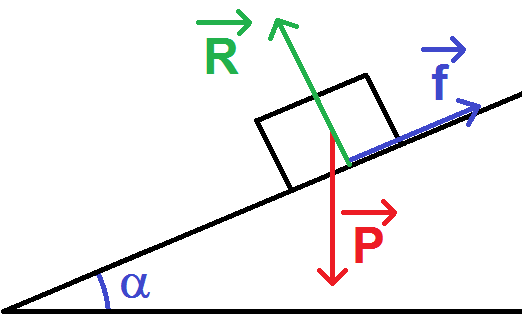
On considère un skieur (représenté par un carré) sur une pente inclinée d’un angle α par rapport à l’horizontale.
Ce skieur est soumis à son poids 
1) Dans un premier temps, le skieur descend la pente à vitesse constante v.
Déterminer ||
2) On néglige désormais f : déterminer 
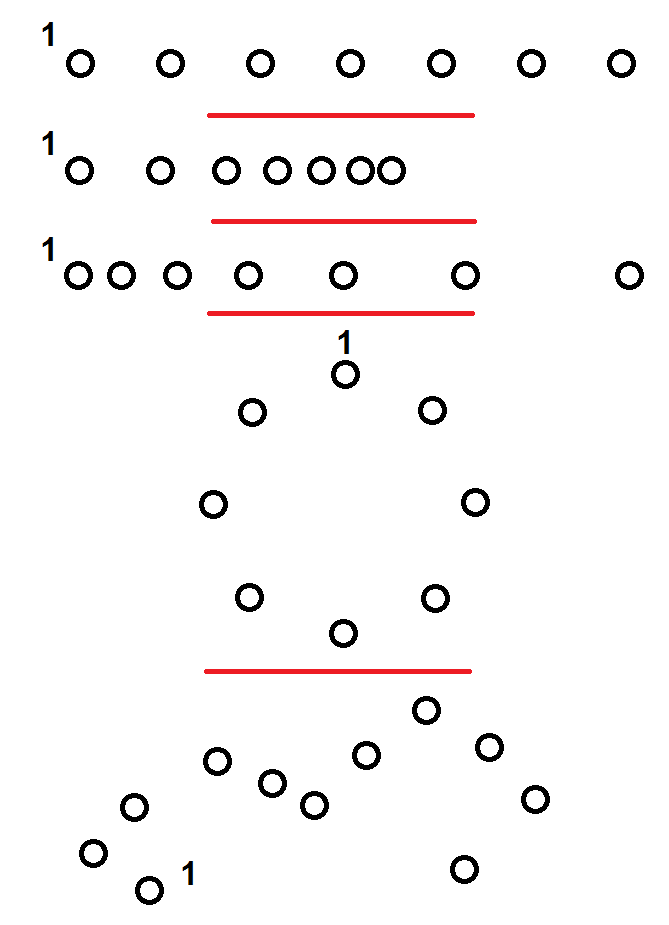
On considère maintenant divers enregistrements de la position d’une balle à intervalles réguliers.
1) Décrire le mouvement dans chacun des cas.
2) Dans chaque cas, les forces se compensent-elles ?
(le 1 indique la position initiale).
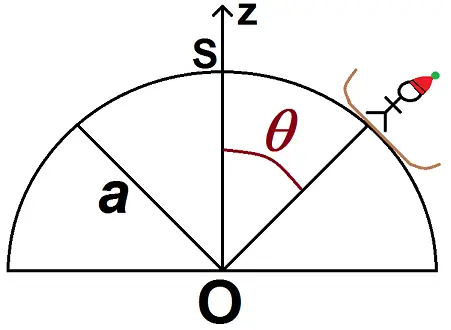
Un enfant glisse sans frottement depuis le sommet S d’un igloo de rayon a.
1) A partir de quel angle θ0 il n’y a plus de contact avec l’igloo ?
2) Quel est le mouvement après cette rupture de contact ?
On considère deux masses m et M reliés par un fil inextensible posé sur une poulie.
On note μd le coefficient de frottement entre la masse m et le plan sur lequel elle repose.
On obtient la schéma suivant :
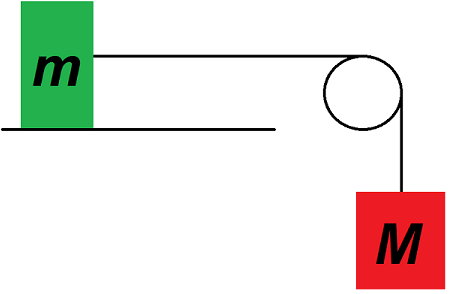
1) Trouver la masse nécessaire M pour que le système se mette mouvement.
2) On suppose maintenant que la masse M vérifie la condition trouvée au 1), et on la lâche d’une hauteur h du sol.
A la fin du mouvement, la masse m s’est décalée vers la droite d’une longueur h + d.
Exprimer μd en fonction des données de l’énoncé (m, M, h et d).
Retour au sommaireHaut de la page
