Sommaire
Introduction
Protons équivalents
Protons voisins
Spectre RMN
Courbe d’intégration
Méthode récapitulative
Exercices
La spectroscopie RMN est une technique basée sur le phénomène de résonance magnétique nucléaire (RMN). Dans le médical on parle d’IRM (imagerie par résonance magnétique), un terme que tu as peut-être déjà entendu.
Cette technique permet par exemple d’identifier des molécules.
On va s’intéresser à des molécules comportant des atomes d’hydrogène H, aussi appelés protons. En effet un noyau d’hydrogène est constitué d’un seul et unique proton (pas de neutron), ce pourquoi dans ce chapitre on parlera de la même chose quand on dira « un proton » ou « un atome d’hydrogène » ou « H ».
Nous allons écrire ces molécules sous forme développé afin de trouver les protons équivalents.
Mais qu’est-ce-que des protons équivalents ?
Ce sont tout d’abord des atomes H qui sont reliés au même carbone.
Prenons cette molécule par exemple
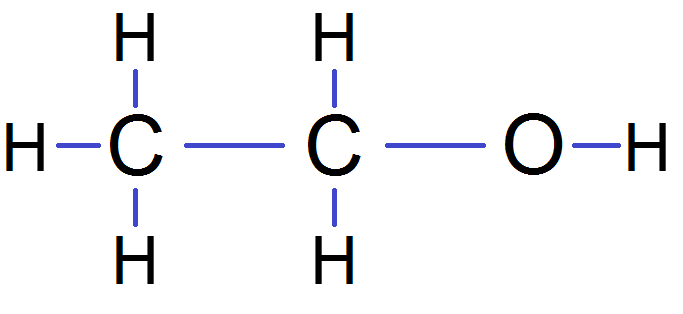
Dans cette molécule, les atomes entourés en rouge sont équivalents car ils sont reliés au même carbone. De même, les H entourés en vert sont équivalents car ils sont reliés au même carbone :
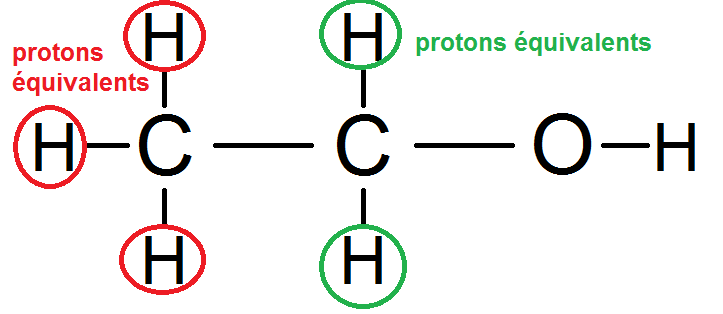
Mais la définition de protons équivalents est plus large, car sont également équivalents les protons ayant le même environnement chimique.
Concrètement, il s’agit des protons qui ont un rôle symétrique dans la molécule.
Prenons cette molécule :
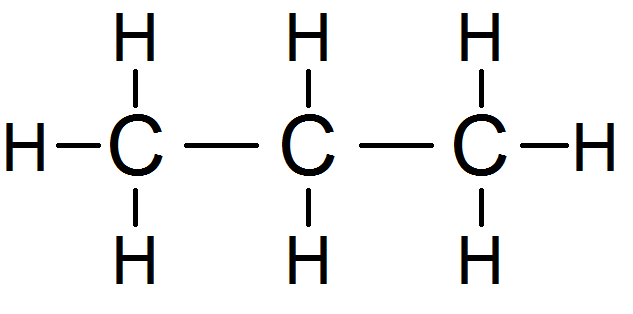
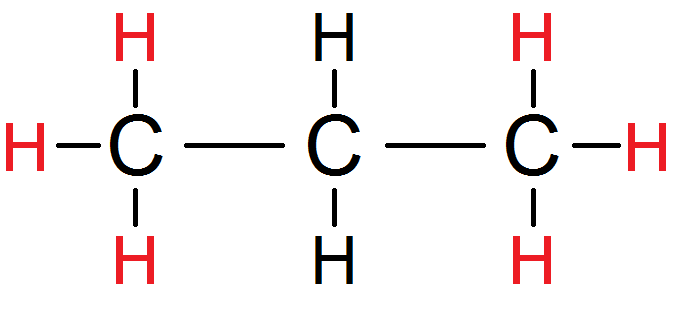
Les trois H du carbone de gauche sont équivalents (on les met en rouge), de même que les 3 H du carbone de droite :
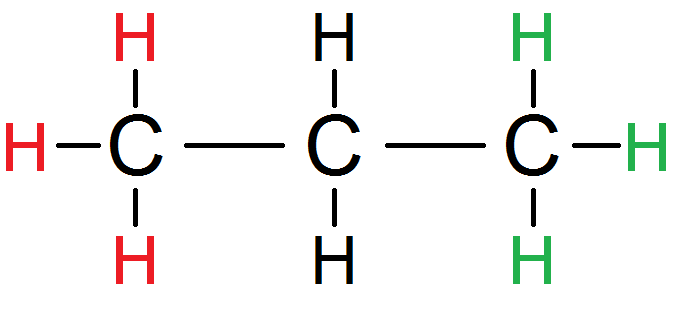
Cependant, ces trois H avec leur atome de carbone ont un rôle totalement symétrique dans la molécule (la molécule serait identique si on échangeait la place du C de gauche et ses 3 H avec le C de droite et ses H) : ils sont donc équivalents entre eux ! On peut donc les mettre d’une seule couleur :
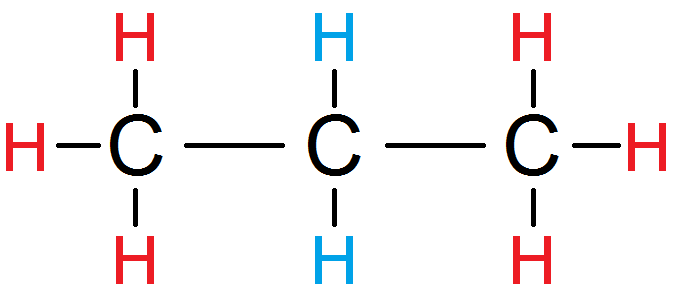
Les deux H du milieu sont équivalents (car reliés au même C) mais n’ont pas de rôle symétrique par rapport aux autres H, ils sont donc d’une autre couleur :
Dans cet autre exemple, les H en rouge sont tous équivalents :
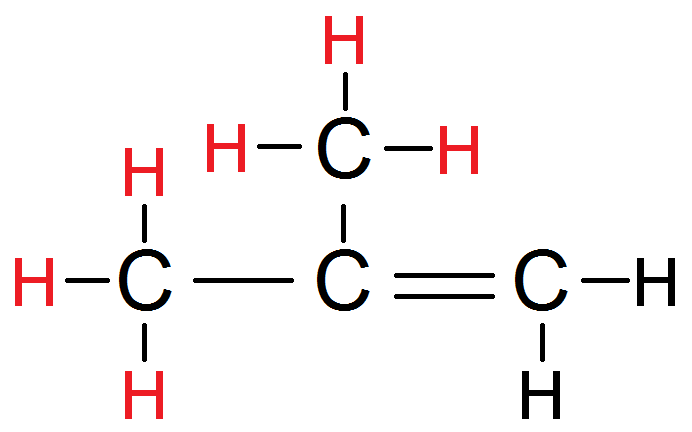
En effet, mettons dans 2 couleurs différentes (pour pouvoir les identifier) les H avec leur carbone :
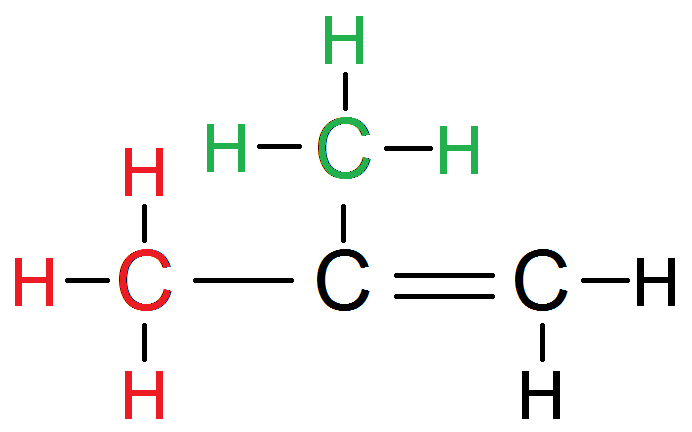
Si on les inverse, on a la même molécule !
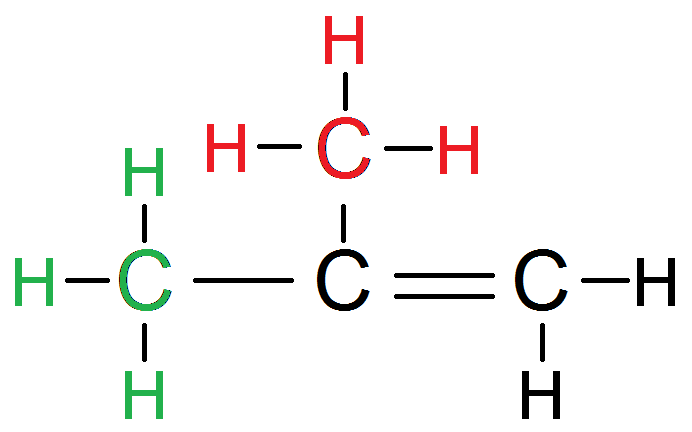
Ces 6 protons sont donc équivalents.
De manière générale, les protons équivalents sont ceux qui ont le même environnement chimique, c’es-à-dire :
– soit ils sont reliés au même carbone
– soit ils ont un rôle symétrique dans la molécule
Remarque : pour plus de simplicité nous mettrons les groupes de protons équivalents d’une même couleur mais sur ta copie tu pourras les entourer avec une même couleur.
Passons maintenant à une autre propriété à connaître : les protons voisins.
Pour chaque groupe de protons équivalents, on va regarder combien de protons voisins ce groupe possède.
Mais qu’est-ce-qu’un proton voisin ?
—
Un proton est voisin d’un autre proton si le chemin pour aller de l’un à l’autre passe par 2 atomes de carbone (donc 3 liaisons).
—
Prenons un exemple :
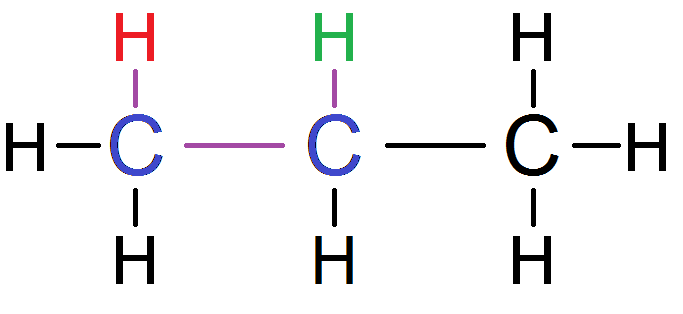
Pour aller du H vert au H rouge, on passe par 2 C (en bleu), et donc 3 liaisons (en violet) : ces protons sont voisins !
En revanche, dans cet exemple :
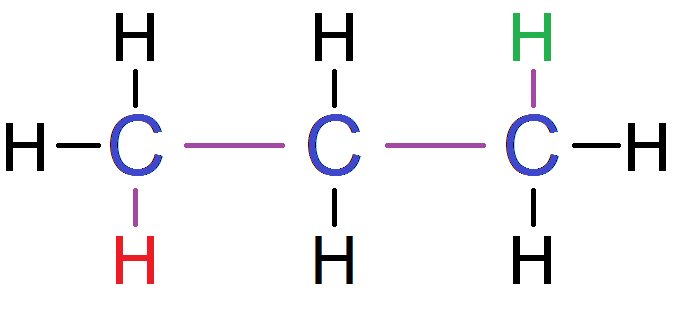
Pour aller du H vert au H rouge, il faut passer par 3 C (et 4 liaisons) : ces protons ne sont PAS voisins.
—
ATTENTION !! Les 2 atomes par lesquels on passe doivent être des atomes de CARBONE!!
Tu auras parfois des atomes d’oxygène :
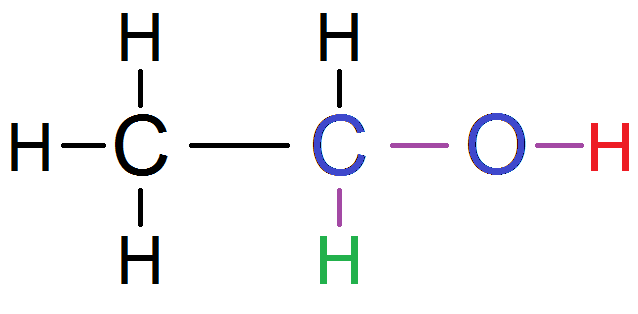
Pour aller du H vert au H rouge on passe bien par 2 atomes (en bleu) et 3 liaisons (en violet), mais les 2 atomes ne sont pas des atomes de carbone, puisqu’il y a un atome d’oxygène !!
Ces deux protons ne sont donc PAS voisins…
—
Maintenant que l’on sait ce qu’est un proton équivalent, il va falloir, pour chaque GROUPE de protons équivalents, trouver combien il a de protons voisins.
Prenons cette molécule : il y a trois groupes de protons équivalents : les rouges, les bleus et le vert.
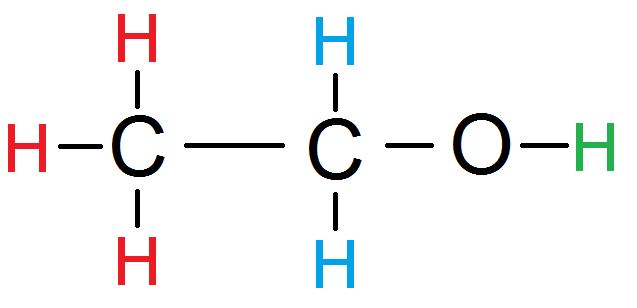
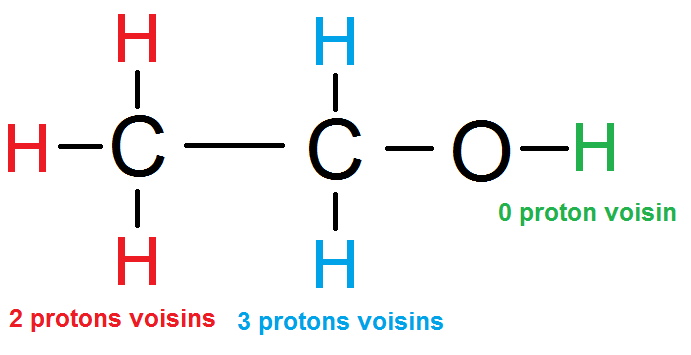
Les H rouges sont protons voisins des H bleus : le groupe bleu a donc 3 protons voisins (les rouges).
Les H bleus sont protons voisins des H rouges : le groupe rouge a donc 2 protons voisins (les bleus).
Le H n’a aucun proton voisin :
Autre exemple :
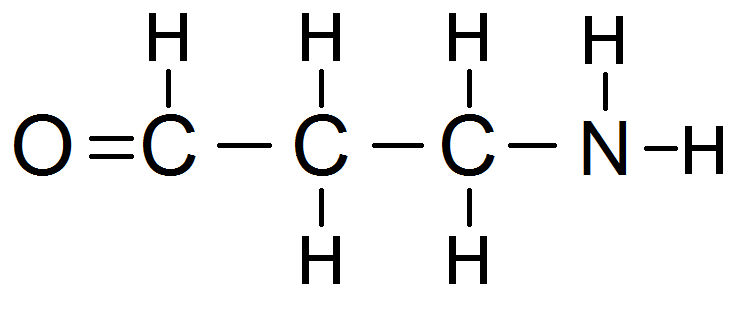
La première étape consiste à rechercher les groupes de protons équivalents :
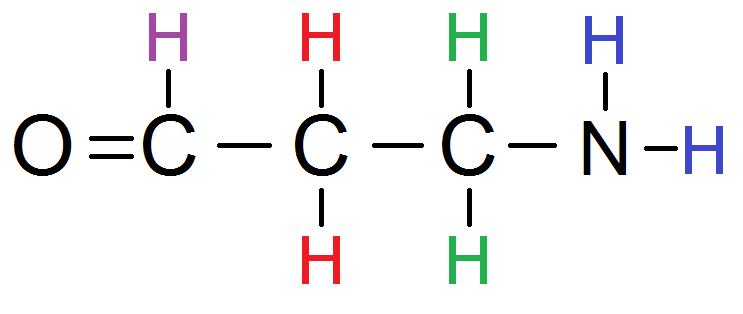
Comme tu le vois il y a 4 groupes de protons équivalents :
le violet (1 proton)
le rouge (2 protons)
le vert (2 protons)
le bleu (2 protons)
Cherchons maintenant les protons voisins de chaque groupe :
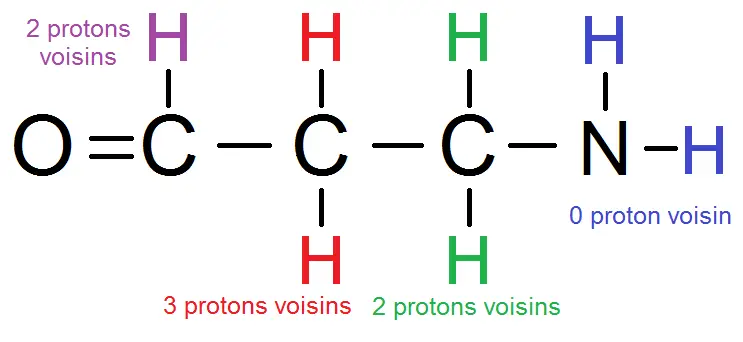
Expliquons un peu cela :
le groupe violet a les 2 H rouges comme protons voisins ;
le groupe rouge a le H violet les 2 H verts, soit 3 protons voisins ;
le groupe vert a les 2 H rouges comme protons voisins (pas les bleus à cause du N !!)
le groupe bleu n’a aucun proton voisin (à cause du N !).
Avec l’habitude tu verras c’est assez simple 
Tu noteras au passage qu’il n’y a aucun lien entre le nombre de protons équivalents d’un groupe et le nombre de protons voisins !
Les groupes bleu, vert et rouge ont par exemple chacun 2 protons équivalents et pourtant ils ont tous un nombre de protons voisins différent.
—
Note bien qu’il n’y a aucun lien entre le nombre de protons équivalents d’un groupe et le nombre de protons voisins qu’il possède !!
—
Avant de voir à quoi cela sert, voyons un piège que tu pourras rencontrer.
Quand on a des H ayant un rôle symétrique, on a vu qu’il étaient équivalents (donc dans le même groupe).
Mais doit-on additionner tous les protons voisins des différents groupes ?
Réponse : NON !
Par exemple sur cette molécule :
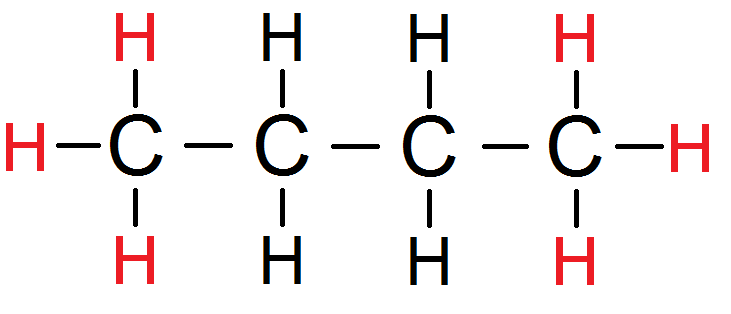
Les H rouges sont équivalents (par symétrie).
Combien ont-ils de voisins ?
En tout ils ont 4 voisins (les 4 H en noir), mais en fait ils n’en ont que 2 !
En effet, puisque les 3 H de droite ont un rôle symétrique par rapport à ceux de gauche, on ne considère qu’un seul des 2 groupes.
On peut prendre n’importe lequel puisqu’ils ont un rôle symétrique.
On prend par exemple les 3 H de gauche : ils ont 2 protons voisins.
Le groupe des 6 protons équivalents rouges a donc 2 protons voisins :
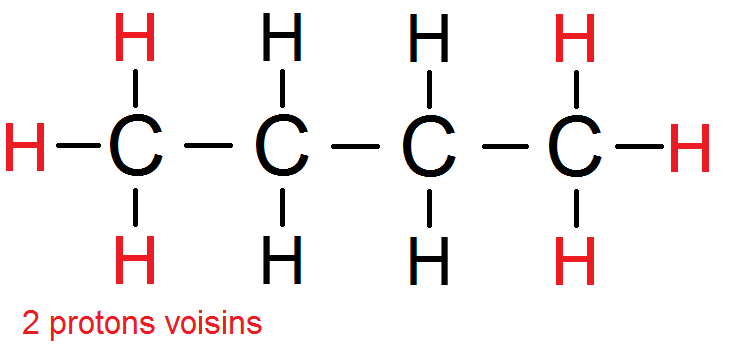
Bien sûr si l’on a 3, 4 5 ou 6 groupes symétriques (on ne sait jamais !), tu ne considère à chaque fois que les protons voisins d’un seul groupe : ce sera le nombre de protons voisins de tout le groupe de protons équivalents.
Sur cette autre molécule on a un groupe de 4 protons équivalents (là encore deux petits groupes symétriques) :
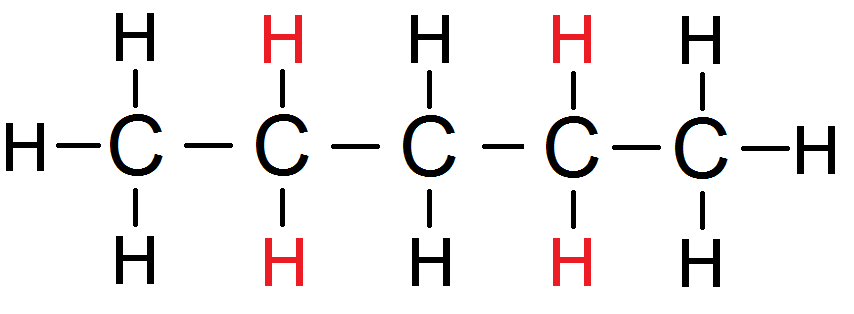
Là encore on ne considère que les protons voisins d’un seul petit groupe, par exemple les 2 H de gauche : ils ont 5 protons voisins.
Le groupe rouge de protons équivalents a donc 5 protons voisins.
Bon c’est bien beau tout ça mais à quoi ça sert ?
C’est ce que nous allons voir tout de suite !
Une fois que l’on a déterminé les groupes de protons équivalents et le nombre de protons voisins de chacun de ces groupes on va pouvoir tracer (ou en tout cas savoir à quoi ressemble) le spectre RMN de la molécule.
Le principe est le suivant :
– chaque groupe de protons équivalents correspond à un signal ;
– chaque signal est composé de pics : s’il y a n protons voisins, il y a n + 1 pics.
Ainsi, si un groupe de protons équivalents a 3 voisins, il sera représenté par un signal de 4 pics.
Si un groupe de protons équivalents a 1 voisin, il sera représenté par un signal de 2 pics.
Si un groupe de protons équivalents a 0 voisin, il sera représenté par un signal d’1 pic etc…
Chaque signal possède un nom en fonction du nombre de pics :
1 pic = singulet
2 pics = duet etc…
Le nom générique pour désigné un signal à plusieurs pics est multiplet.
| Nombre de protons voisins | Nombre de pics | Nom du multiplet |
| 0 | 1 | Singulet |
| 1 | 2 | Doublet |
| 2 | 3 | Triplet |
| 3 | 4 | Quadruplet |
| 4 | 5 | Quintuplet |
| 5 | 6 | Hexuplet |
| 6 | 7 | Heptuplet |
Retiens bien ces noms car ils pourront t’être demandé en contrôle !
—
ATTENTION ! Le nombre de pics est uniquement lié au nombre de protons voisins et n’a aucun lien avec le nombre de protons équivalents…
—
Voyons comment cela se traduit dans le spectre : prenons la molécule suivante, on a précisé le nombre de protons voisins de chaque groupe (tu peux t’entraîner à trouver les groupes et le nombre de voisins de chaque groupe  )
)
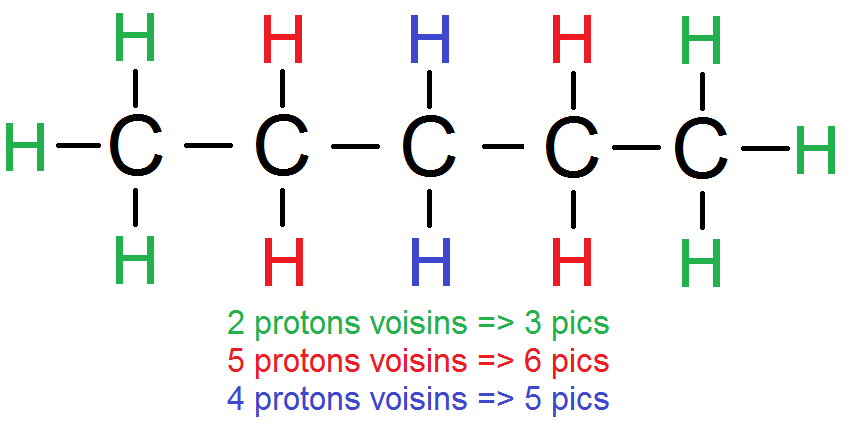
On obtient le spectre suivant :
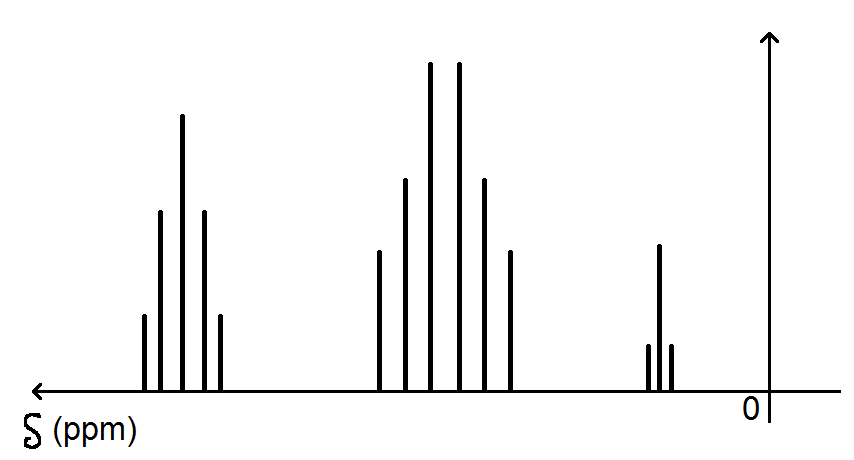
Tout d’abord au niveau du repère, il est un peu particulier car l’abscisse va de la droite vers la gauche avec le 0 à droite (ben oui c’est comme ça…).
L’axe des abscisses représente le déplacement chimique noté δ, en ppm (parties par millions). Ne te casse pas trop la tête ça ne sert à rien à ton niveau de savoir à quoi cela correspond 
Pour l’axe des ordonnées idem, on ne s’en préoccupe pas (c’est toujours ça en moins !).
Au niveau des signaux, tu vois que l’on a 3 signaux :
celui de gauche comporte 5 pics : il s’agit du groupe de protons bleus ;
celui du milieu comporte 6 pics : il s’agit du groupe de protons rouges ;
celui de droite comporte 3 pics : il s’agit du groupe de protons verts.
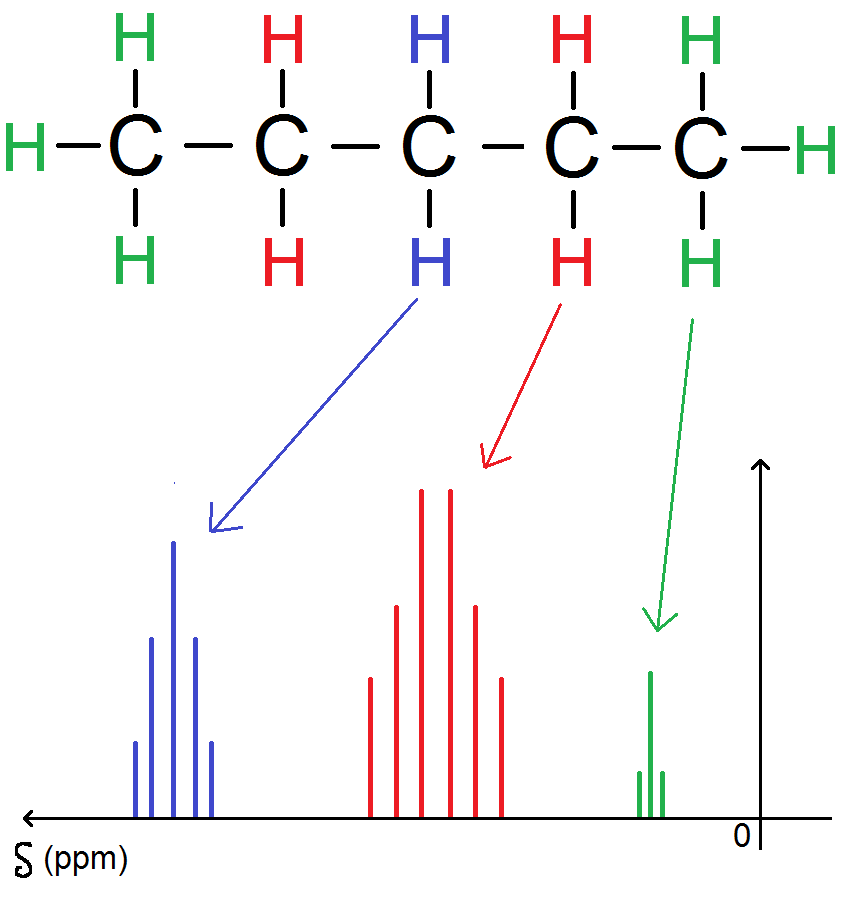
Au niveau de la position de chaque groupe de pics (à gauche, à droite, au milieu etc…) ne t’en préoccupe pas !
En fait, tu n’auras jamais à tracer toi-même le spectre :
– soit on te donnera une molécule et plusieurs spectres et tu devras choisir le bon spectre
– soit on te donnera un spectre et plusieurs molécules et tu devras choisir la bonne molécule
Cela se fera par rapport au nombre de signaux et au nombre de pics de chaque signal : nous verrons cela dans les exemples !
En réalité les pics ne seront pas des bâtons comme dans le graphique ci-dessus mais nous ferons comme cela dans tout le chapitre afin que ce soit plus clair.
En plus des signaux avec les pics, on va rajouter une dernière chose sur le spectre : la courbe d’intégration.
On a vu que le nombre de pics de chaque signal était lié uniquement au nombre de protons voisins.
La courbe d’intégration sera elle uniquement liée au nombre de protons équivalents de chaque groupe.
Au niveau de chaque signal (qui correspond à un groupe de protons équivalents), une courbe va monter verticalement.
La hauteur de la courbe sera proportionnelle au nombre de protons équivalents du groupe en question.
Si par exemple un groupe a 2 protons équivalents et un autre 6 (donc 3 fois plus), la hauteur de la courbe du groupe de 6 protons sera 3 fois plus grande que celle du groupe de 2 protons.
Si l’on reprend l’exemple ci-dessus, on avait 3 groupes de protons équivalents :
le groupe bleu a 2 protons équivalents
le groupe rouge a 4 protons équivalents (2 fois plus que le groupe bleu)
le groupe vert a 6 protons équivalents (3 fois plus que le groupe bleu)
La courbe va monter a une certaine hauteur au niveau du signal bleu.
Elle va monter 2 fois plus au niveau du signal rouge.
Elle va monter 3 fois plus au niveau du signal vert.
On obtient quelque chose qui ressemble à ça :
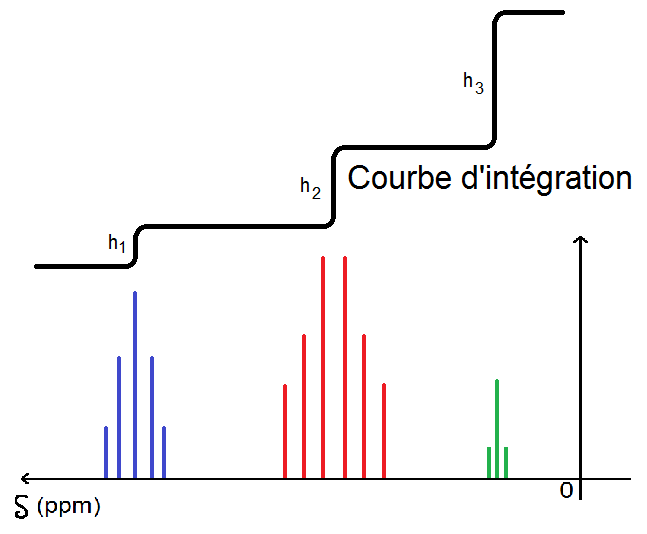
On a mis la courbe d’intégration au-dessus des signaux pour que ce soit plus lisible mais elle peut être mise à n’importe quelle hauteur, elle est parfois superposée aux signaux (c’est un peu moins lisible…).
Si l’on note h1, h2 et h3 les hauteurs de la courbe comme sur le graphique, on a, d’après ce qui a été dit plus haut :
h2 = 2h1
h3 = 3h1
Généralement on te donnera la courbe d’intégration et tu devras mesurer la hauteur de chaque « montée », ce qui te donnera une indication sur le nombre de protons équivalents de chaque groupe.
En réalité, comme les hauteurs sont proportionnelles, ce sera plutôt les proportions de protons que tu auras grâce à la courbe d’intégration.
Concrètement, dans l’exemple ci-dessus, tu sais que le groupe rouge a 2 fois plus de protons équivalents que le groupe bleu, et que le groupe vert en a 3 fois plus, mais tu ne sais pas combien !
Si le groupe bleu en a 5 par exemple, le groupe rouge en aura 10 et le groupe vert 15.
Si le groupe bleu en a 6 par exemple, le groupe rouge en aura 12 et le groupe vert 18 etc…
Il faudra donc regarder le nombre TOTAL de H que possède la molécule.
Il est alors possible de faire une équation faisant intervenir la proportionnalité, nous verrons cela dans les exercices.
Prenons un autre exemple : on a la courbe d’intégration suivante, sur laquelle on a noté les longueurs mesurées (que tu mesureras à la règle sur les graphiques que tu auras en contrôle ou au bac) :
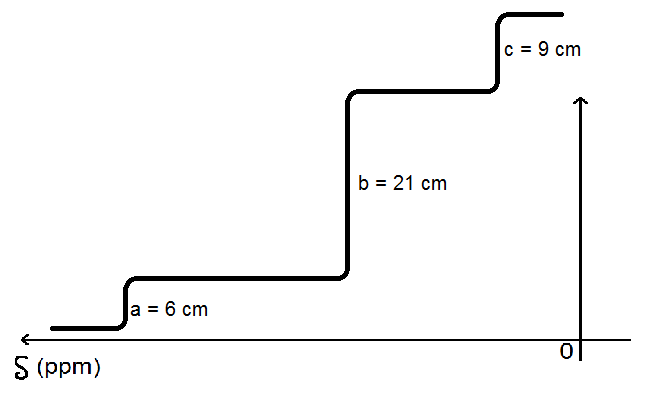
Il faut trouver des relations entre les différentes longueurs.
On remarque que c = 1,5 a (car 9 = 1,5 × 6)
et b = 3,5 a (car 21 = 3,5 × 6).
On sait donc que :
– le groupe correspondant à c aura 1,5 fois plus de H que le groupe correspondant à a ;
– le groupe correspondant à b aura 3,5 fois plus de H que le groupe correspondant à a.
Si a représente 1 H, b représentera 1,5 H : impossible (on ne peut pas avoir des demi protons!).
Si a représente 2 H, b représentera 7 H et c représente C H : c’est possible.
On aurait alors un groupe de 2 protons équivalents, un groupe de 7 et un groupe de 3, soit 12 H dans la molécule.
Si a représente 4 H, b représentera 6 H et c représente 14 H : c’est possible.
On aurait alors un groupe de 4 protons équivalents, un groupe de 6 et un groupe de 14, soit 24 H dans la molécule.
On peut faire le même raisonnement avec d’autres valeurs évidemment.
Ainsi, tout va dépendre du nombre total de H dans la molécule !
Nous verrons dans les exercices des applications encore plus concrètes 
Pour conclure, nous allons résumer les points essentiels à connaître et récapituler la méthode permettant d’associer une molécule à une graphe :
Les protons équivalents sont ceux qui ont le même environnement chimique, c’est-à-dire :
– soit ils sont reliés au même carbone ;
– soit ils ont un rôle symétrique dans la molécule.
Un proton est voisin d’un autre proton si le chemin pour aller de l’un à l’autre passe par 2 atomes de carbone (donc 3 liaisons).
En cas de symétrie, on ne prendra en compte que les voisins d’un seul sous-groupe.
Chaque groupe de protons équivalents correspond à un signal ;
Chaque signal est composé de pics : s’il y a n protons voisins, il y a n + 1 pics.
La hauteur de la courbe d’intégration est proportionnelle au nombre de protons équivalents du groupe en question.
Afin de relier une graphique (courbe d’intégration et/ou signaux avec des pics) à une molécule:
– le nombre de groupes de protons équivalents correspond au nombre de signaux ;
– le nombre de pics indique le nombre de protons voisins de chaque signal
(attention : 8 pics = 7 protons voisins, 3 pics = 2 protons voisins etc…) ;
– les hauteurs relatives de la courbe d’intégration donnent des indications sur la proportion de protons équivalents des groupes.
Nous verrons dans les exercices comment appliquer ce principe dans les 2 sens (associer une molécule au bon graphique si on a plusieurs graphiques, ou associer un graphique à la bonne molécule si on a plusieurs molécules).
Fini la théorie, place aux exercices !
Les exercices sur ce chapitre sont disponibles en cliquant sur ce lien !



Merci beaucoup
merci beaucoup
Cours extrêmement bien expliqué et contenu complet ! Bravo et merci
Bonjour,
je vous remercie infiniment pour ce cours parfait
ps: il y a une erreur quand vous dites que si A=2H alors B=3H et C=7H vous avez inversez le B et le C 😉
Merci beaucoup ! L’erreur a été corrigée 🙂
Merci infiniment ! J’ai ENFIN compris cette leçon !
merci infiniment
Merci beaucoup ! Je peux enfin y voir clair ! La RMN n’est finalement qu’un jeu d’enfants !
Oui en effet ! 🙂
Cours très bien expliquer, merci infiniment 🙏🙏
Merci !! 🙂
La leçon est excellente; elle m’a permis d’apprendre facilement mon cours, je vous en remercie!
Magnifique ce cours!!! très bien expliqué au détails près. Avec ça, la RMN ne sera plus qu’un jeu d’enfants!!!
Merci beaucoup ! 🙂
Divin ! Merci !